Jednoliko kružno gibanje

Budući da se gibanje odvija po nekom putu nameće se nekako potreba da o putu saznamo sve što je važno za proučavanje gibanja. Pri tome će nas svakako zanimati duljina puta. A važno je znati i to je li put ravan ili zakrivljen, da li se uspinje po kosini ili se spušta, kakvo je trenje itd. Kod kružnog gibanja put je kružnica. Stoga ćemo se podsjetiti osnovnih pojmova..

 Krug i kružnica  su geometrijski pojmovi koje treba razlikovati, jer to nije isto. Krug je dio ravnine, dakle geometrijski lik, a kružnica je zakrivljena crta koja omeđuje krug. Do pogrešnog shvaćanja tih pojmova dolazi uglavnom zato jer se u svakodnevnom govoru riječ krug rabi kad se misli na kružnicu npr.: "Vozili smo se u krug vračajući se stalno na isto mjesto."
    Da bismo upamtili razliku između kruga i kružnice predočit ćemo si slijedeću sliku : Iz komada papira možemo izrezati krug, ako škarama režemo po kružnici.(Doduše tako izrezani "krug" ima debljinu papira, ali je ta dimenzija tako mala da je možemo zanemariti i smatrati izrezani komad geometrijskim likom) (Sl. 1.)

U opisivanju gibanja po kružnici trebat će nam neki nazivi za točnije sporazumijevanje.

 

a) Kružnica je skup točaka ravnine koje su jednako udaljene od jedne točke u istoj ravnini - koju zovemo središte, a na crtežima ćemo tu točku označavati slovom S. (Sl.2.)

 

 

b) Udaljenost od središta S do bilo koje točke na kružnici zove se polumjer ili radijus, a na crtežima ćemo tu dužinu označavati slovom r. (Sl.3.)

 

 

c) Dužina koja spaja dvije točke na suprotnim stranama kružnice a prolazi središtem zove se promjer ili dijametar. Tu dužinu ćemo označavati kao 2r ili d. (Sl 4.)

 

Za opisivanje kružnog gibanja još je važno je i da razumijemo što je to broj π (grčko slovo pi). Svi znamo koliki je iznos toga broja (π = 3.14.....), ali treba znati odakle potječe taj broj i zašto iznosi upravo toliko. Kako se dolazi do njega i u kakvoj je on vezi s kružnicom.

Da bi odgovorili na postavljena pitanja nacrtat ćemo kružnicu i zamisliti da je načinjena od savitljive niti ili žice, tako da ju na jednom mjestu možemo presjeći škarama. (Sl.5a) Kad je presječena izravnajmo ju i promatrajmo tako ispruženu kružnicu.(Sl 5b) Sad možemo mjeriti njenu duljinu primjenjujući različita mjerila. Npr. centimetar, inč, lakat itd. Možemo čak uzeti bilo koji predmet i stavljajući ga uz ispruženu kružnicu određivati koliko je takovih predmeta dugačka kružnica. Pa ako, recimo, kao mjerilo uzmemo gumicu za brisanje, možemo se pitati koliko "gumica" je dugačka ispružena kružnica? (Sl. 5c)
    Ako duljinu ove kružnice izmjerimo centimetrom vidjet ćemo da je dugačka približno 7 cm. Ako ju pak mjerimo npr. gumicom za brisanje dobit ćemo duljinu od oko "3 gumice". Dakle iznos će svaki put ovisiti o upotrebljenoj mjeri, stoga ćemo svaki put dobit drugačiji broj.

Mjerenje kružnice njenim promjerom

A sad ćemo za mjeru uzeti promjer ili dijametar kružnice. Možemo promjer uzeti u otvor šestara (Sl. 6.) i nanositi ga na ispruženu kružnicu. (Sl. 7) Kolika god da je kružnica uvijek će promjer na nju stati 3,14... puta. Tim smo postupkom promjer proglasili mjernom jedinicom. Kaže se još da smo normirali mjeru.

Dakle svaka je kružnica dugačka točno 3,14... svojih promjera. Taj broj nije racionalan pa umjesto preostalih decimalnih mjesta stoje točkice. Zato ćemo odsad za  njegovo označavanje upotrebljavati grčko slovo π.

Zašto je omjer između opsega kružnice i njenog promjera upravo 3,14.. to nitko ne zna, ali se divimo činjenici da je to uvijek kod svake kružnice tako.

Duljina kružnice ili opseg je dakle

 O = 2rπ  

 

 

Ova činjenica o opsegu ili duljini kružnice toliko je značajna da ćemo ju još i pokusom dokazati.

Uzet ćemo bilo kakovu okruglu posudu (npr. lončić ili zdjelu). Zatim ćemo oko posude obaviti konac ili neku nit, kao što rade krojači kad uzimaju mjeru za opseg oko prsa ili struka obavijajući krojački metar oko tijela osobe za koju šiju. (Sl. 8.)  Nakon toga ćemo nit ispružiti po stolu i zabilježiti njen početak i kraj. Tako određenu dužinu izmjerit ćemo promjerom posude (Sl. 9.)

Vidimo da u opseg stanu uvijek tri cijela promjera i još malo ostane. To "malo" je onih 0,14... promjera. Ponovimo li ovaj pokus s bilo kojim drugim okruglim predmetom rezultat će uvijek biti isti.

 

Kad se okruglo tijelo (kotač, bačva, i sl.) kotrlja po nekoj podlozi bez klizanja onda se sa svakim okretom  "odmota" po podlozi duljina  opsega, a on je uvijek 3,14 puta dulji od promjera. Pa sa svakim okretom tijelo prijeđe put 2rπ. (Sl. 10.)

 

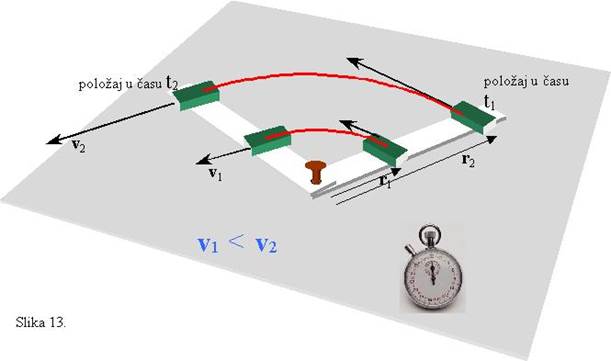
Stavimo na stol ravnalo koje na jednom kraju ima rupu i kroz tu rupu zabijemo čavlić, a na drugi kraj ravnala položimo neko tijelo, na primjer gumicu za brisanje. Tada možemo, gurajući ravnalo rukom, postići da se gumica giba po kružnoj putanji. (Sl. 11.)

Slično se događa kad jedan krak šestara zabodemo u podlogu a drugi krak jednoliko kruži oko te nepomične točke opisujući kružnicu. U različitim trenucima t₁, t₂, t₃, ... itd. tijelo (gumica) će se naći na različitim položajima svoje kružne putanje. U pojedinim razdobljima prelazit će putove koji su jednaki duljini kružnog lûka između pojedinih položaja. Kod gibanja po kružnici tijela imaju brzinu baš kao i kod gibanja po ravnim putanjama. 

Dakle, i kod kružnog gibanja brzina je omjer prijeđenog puta i vremena, samo što je put savijen u lûk kružnice duljine Δs. (Sl. 12.)

Trajanje gibanja dobit ćemo ako od konačnog vremena t₂ oduzmemo početno vrijeme t₁. Početno i konačno vrijeme očitamo sa zaporne ure kojom mjerimo trajanje gibanja. Odnosno kažemo da je vrijeme gibanja razdoblje ili interval Δt = t₂ - t₁, a brzina je omjer puta i vremena.

To je obodna brzina tijela koje jednoliko kruži. Budući da će u istim vremenskim razmacima tijelo prevaljivati jednake putove onda će tako dobiven iznos brzine biti isti bez obzira na kojem dijelu kružnice promatramo gibanje.

Obodna brzina je vektor, što znači da osim iznosa ima i smjer u prostoru. Njen smjer je u svakom trenutku gibanja takav da s polumjerom zatvara pravi kut. Kažemo da je vektor brzine okomit na polumjer putanje ili da je brzina tangencijalna jer leži na pravcu koji je tangenta kružne putanje.

Jednoliko kruženje odvija se tako da tijelo stalno  iznova prelazi isti put, a to je kružnica po kojoj se giba. Budući da se sa svakim obilaskom te kružne putanje gibanje ponavlja, možemo brzinu računati tako da načinimo omjer između duljine čitave kružnice i trajanja jednog obilaska po njoj. Dobit ćemo pri tome isti broj kao i kad smo u omjer stavljali mali odsječak puta Δs i pripadajuće vrijeme Δt.

 

Time što smo brzinu odredili  upravo na jednom obilasku cijele kružnice normirali smo vrijeme, tj. veličina T u nazivniku postala je mjera za put duljine opsega. Vrijeme jednog obilaska kružnice mjereno u sekundama naziva se "period"

Iz ove formule se vidi da je obodna brzina razmjerna polumjeru kružnice. Jer, da smo našu gumicu stavili na ravnalo bliže središtu vrtnje ona bi u istom vremenu prevalila kraći put. Odnosno tijelo koje se s istim periodom giba po kružnici većeg polumjera ima i veću obodnu brzinu (Sl. 13)

S periodom je u tijesnoj vezi jedna važna fizikalna veličina koju zovemo frekvencija.

 Period je trajanje ili vrijeme jednog obilaska u sekundama, a frekvencija je broj koji nam kaže koliko puta tijelo obiđe kružnicu u jednoj sekundi. Period i frekvencija su međusobno recipročne veličine. Na primjer, ako tijelu treba 0,2 sekunde (ili 1/5 sekunde) da obiđe kružnicu, onda u jednoj sekundi tijelo učini 5 obilazaka. Ili, ako period iznosi 4 sekunde onda tijelo u jednoj sekundi izvrši 1/4 okreta, pa kažemo da je frekvencija 0,25 s^-1. Jedinica za frekvenciju je [s^-1], ili Hertz [Hz] 

Sad kad znamo što je frekvencija, možemo  izraz za obodnu brzinu pisati u još jednom obliku, tako da opseg kružnice umjesto dijeljenja s periodom pomnožimo s frekvencijom

Kod kružnog gibanja tijelo osim obodne brzine ima još jednu veličinu koju zovemo kutna brzina. Kako se već iz samog naziva može nazrijeti kutna brzina je u vezi s kutovima, pa je neophodno da kutove znamo mjeriti različitim mjerama. Jednu od mjera već poznajemo, to su stupnjevi (krug podijeljen na 360 dijelova). Druga mjera za kut, koju trebamo znati su radijani. Postoje još i gradi (krug podijeljen na 400 dijelova), ali o njima nećemo govoriti jer se ta stara njemačka mjera više ne koristi. Sve tri mjere postoje na džepnim kalkulatorima i treba dobro paziti koja je mjera odabrana tipkom DRG .

Kutove smo navikli mjeriti u stupnjevima. Oni se dobiju tako da krug podijelimo na 360 jednakih dijelova. Jedan takav dio ravnine je stupanj.

Radijani su mjera za kut koju ćemo također dobiti dijeljenjem kruga ali na drugi broj dijelova. Evo kako:

Nacrtat ćemo kružnicu pomoću šestara. Spojimo polumjerom središte s bilo kojom točkom na kružnici, a zatim iz te točke nastavimo nanositi polumjer presijecajući kružnicu šestarom. (Sl. 14)

S koliko ćemo takvih koraka  ponovo doći u početnu točku? Očito sa šest koraka. Uostalom šestar se i zove tako jer pomoću njega možemo krug podijeliti na šest jednakih dijelova. Svatko će se sjetiti "cvjetića" koje djeca rado konstruiraju kad se upoznaju sa šestarom.

Polumjer položen na lûk kružnice

Polumjer položen šestarom pruža se kao tetiva lûka. No mi ćemo zamisliti da je polumjer načinjen od neke niti ili konca, tako da ga možemo položiti na samu crtu kružnice (vidi sliku 15). Sad je polumjer postao lûk. Spojimo li krajeve tog lûka sa središtem kružnice bit će time određen kut od jednog radijana (Sl. 16).

 

STUPNJEVI		RADIJANI
0°	=	0
90°	=	π/2
180°	=	π
270°	=	3π/2
360°	=	2π

Kad smo govorili o broju π vidjeli smo da promjer može stati na kružnicu 3.14… puta, stoga je očito da će  polumjer koji je upola kraći stati na kružnicu dvostruko više puta, tj. 6,28…ili 2π puta. A budući da svaki lûk duljine polumjera određuje kut od jednog radijana imat će puni krug 6,28…ili 2π radijana. Sad znamo još jednu mjeru za kutove pa možemo lako pretvarati stupnjeve u radijane i obrnuto pomoću tablice:

 

 

 

 

Za pojam kutne brzine u sljedećem poglavlju važno je upamtiti da puni kut ima 2π radijana.

 

 

Vratimo se sada kutnoj brzini. Tijelo koje se giba po zakrivljenoj putanji uvijek ima neku udaljenost od središta zakrivljenosti. Općenito se ta udaljenost mijenja, no kod gibanja po kružnici ona je stalna. Vektor koji se pruža od središta zakrivljenosti putanje do tijela na toj putanji naziva se "vektor pratilac" ili "radijus-vektor". Vrh tog vektora stalno prati tijelo tijekom gibanja, a početak je vezan za središte zakrivljenosti. Kako se vektor pratilac vrti zajedno s tijelom tako njegova dužina prelazi ravninom gibanja i pri tom "prebriše" određeni kut. (Slika 17)

U različitim trenucima t₁, t₂, t₃, ... itd. tijelo (gumica) će se naći na različitim položajima svoje kružne putanje. U pojedinim razdobljima vektor pratilac prebrisat će kutove određene duljinom kružnog lûka između pojedinih položaja. Kutna brzina je omjer prebrisanog kuta Δφ i vremena Δt, a označava se grčkim slovom omega. ω (Sl. 18)

 

Kao primjer kutne brzine poslužit će nam brisač vjetrobranskog stakla na vozilu. Ako od jednog do drugog krajnjeg položaja brisač, na primjer, prebriše kut od 120°, a za to mu je potrebno recimo 2 sekunde, onda je njegova kutna brzina 60° u sekundi.

 

To je kutna brzina tijela koje jednoliko kruži. Budući da će u istim vremenskim razmacima radijus-vektor prebrisati jednake kutove onda će tako dobiven iznos kutne brzine biti isti bez obzira na kojem dijelu kružnice promatramo gibanje.

Kutna brzina je vektor. U svakom trenutku taj vektor zatvara pravi kut i s polumjerom i s obodnom brzinom. Kažemo da je vektor brzine okomit na ravninu putanje ili da kutna brzina leži na pravcu koji je os vrtnje tijela. Smjer se određuje pravilom desne ruke – kad prsti pokazuju smjer obodne brzine palac pokazuje smjer kutne brzine.

Budući da se sa svakim obilaskom kružne putanje gibanje ponavlja, možemo kutnu brzinu računati tako da načinimo omjer između punog kuta i vremena potrebnog da se on prebriše, a to je trajanje jednog obilaska po kružnici. Dobit ćemo pri tome isti broj kao i kad smo u omjer stavljali mali odsječak kuta Δφ i pripadajuće vrijeme Δt. Sad kad znamo što su to radijani puni kut ćemo mjeriti tom mjerom. Radijani nemaju posebnu oznaku za jedinicu, stoga se u formulama ne piše [rad] niti išta drugo. Jedinica za kutnu brzinu je [s^-1].     

Time što smo kutnu brzinu odredili  upravo na jednom obilasku cijele kružnice normirali smo vrijeme na isti način kao i kod obodne brzine. Iz ove formule se vidi da kutna brzina ne ovisi o polumjeru kružnice. Jer, da smo našu gumicu stavili na ravnalo bliže središtu vrtnje njezin bi radijus-vektor u istom vremenu prebrisao isti kut. Odnosno
tijela koja se s istim periodom gibaju po kružnicama različitih polumjera imaju jednaku kutnu brzinu (Sl. 19)

Izraz za kutnu brzinu možemo pisati u još jednom obliku, tako da puni kut
(u radijanima) umjesto dijeljenja s periodom pomnožimo s frekvencijom:

 

Izveli smo izraze za obodnu i kutnu brzinu, pa pogledajmo kakva je veza među tim izrazima i kako se znajući jednu od tih brzina može izračunati ona druga. To će nam biti od velike koristi u rješavanju zadataka.

OBODNA BRZINA                                 KUTNA BRZINA

U izrazu za obodnu brzinu nalazi se izraz 2π/T koji možemo zamijeniti znakom ω jer je to kutna brzina.

 

Zadatak. Na crtežu desno prikazan je lančani prijenos kod bicikla. Na zupčanicima koji se okreću su dva zupca obojena crveno. Koji od tih zubaca ima veću kutnu, a koji obodnu brzinu?

Odgovor

• Obzirom da lanac povezuje zupce na oba zupčanika oni imaju jednake obodne brzine, odnosno brzinu koju ima sam lanac.
  Kutna brzina se može razumjeti i kao broj okretaja u sekundi, to znači da zubac na manjem zupčaniku ima veću kutnu brzinu.
  

Razmatrat ćemo kruženje stalnom kutnom brzinom, odnosno gibanje sa stalnim brojem obilazaka u sekundi. Mogli bismo pomisliti da za ove uvjete vrijedi I. Newtonov zakon, ali on se odnosi na jednoliko gibanje po pravcu, a ne po kružnici. Gibate li se po kružnici možete imati stalan iznos brzine, ali smjer brzine sigurno neće biti stalan jer se on kod kružnog gibanja neprekidno mijenja.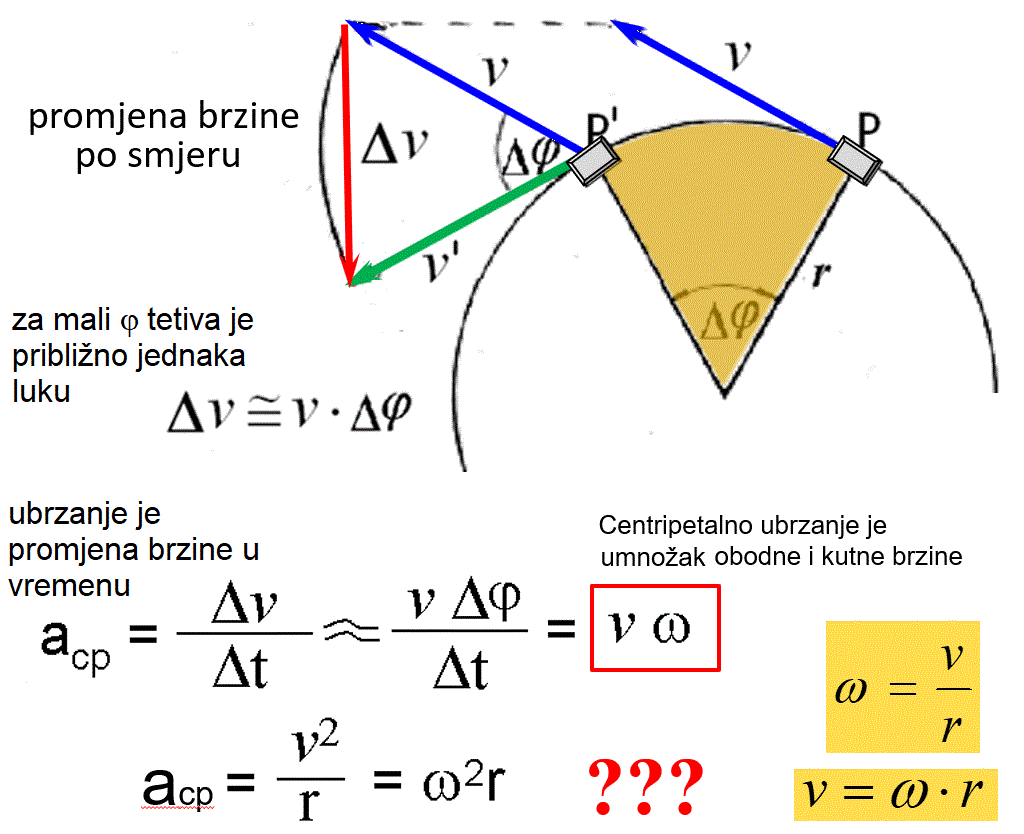

Tijekom vrtnje tijelo se stalno ubrzava prema središtu kružnice. Unatoč tom stalnom ubrzanju tijelu se ne povećava iznos brzine niti se ono približava središtu. Ubrzanje se očituje jedino u tome, što tijelo skreće smjer svoje brzine prema središtu.
Promatrajmo brzinu tijela na početku i na kraju kratkog razdoblja Δt. Na početku je tijelo u točki P i ima brzinu v. Poslije toga je u točki P' i ima brzinu v'. To nisu isti vektori. Translatiramo li vektor v, bez zakretanja, tako da mu se hvatište poklapa s hvatištem od v' vidjet ćemo da među njima postoji razlika Δv. U promatranom razdoblju smjer vektora brzine promijenio se za isti kut Δφ koji je prebrisao i radijus vektor r.

Da brzinu zakrenemo za toliki kut, moramo joj prema središtu kružnice dati prirast jednak Δv. No veličinu tog vektora nećemo računati izravno nego ćemo je zamijeniti lûkom koji je opisao vrh vektora obodne brzine kad se je iz položaja u času t₁ zakrenuo u položaj u času t₂. Za male kutove to će biti dobro približenje. Toliko je približno velik lûk između strelica v i v', koje na crtežu predočuju brzine na početku i kraju razdoblja Δt. Tu promjenu brzine sila je proizvela u promatranom vremenu Δt. Dakle, omjer između promjene brzine i tog vremena upravo je jednak kružnoj (centripetalnoj) akceleraciji:

a_cp =

Δv / Δt

≈

v Δφ / Δt

Omjer kuta Δφ i vremena Δt jednak je kutnoj brzini ω odnosno omjeru između punog kuta kružnice (u radijanima) 2π i trajanja T jednog cijelog okretaja.

Stoga je centripetalno ubrzanje jednako umnošku obodne i kutne brzine.

a_cp = v ω

odnosno, ako uvedemo zamjene v = ω r  i  ω = v/ r

a_cp =

v² / r

= ω² r

Ova jednakost je na prvi pogled proturječna. Naime ne možemo odmah reći je li centripetalno ubrzanje veće kad je tijelo bliže središtu vrtnje ili kad je dalje od njega. Za jedno tijelo u kružnom gibanju ubrzanje se doista može iskazati na oba načina, obrnuto razmjerno polumjeru i razmjerno polumjeru, ovisno o tome uzimamo li obodnu ili kutnu brzinu. Ali ako uspoređujemo centripetalno ubrzanje za dva tijela na različitim polumjerima, na primjer, dva automobila koji ulaze u zavoje istim (obodnim) brzinama, onaj na zavoju manjeg polumjera ima veće centripetalno ubrzanje. Međutim, kada usporedimo, primjerice, dva drvena bloka na okretnoj ploči gdje su im kutne brzine jednake, tada blok na većem polumjeru ima veće centripetalno ubrzanje.

Centripetalno ubrzanje obrnuto je razmjerno polumjeru

Ovo je dosta zorno. Zamislimo da se polumjer zavoja ceste povećava. Tada se sve manje mijenja smjer brzine prema središtu. U granici beskonačnog polumjera tijelo se kreće po pravcu, i centripetalnog ubrzanja nema. Ovisnost centripetalnog ubrzanja o kvadratu brzine možemo također lako uvidjeti ako pomislimo da se smjer brzine to brže mijenja što se čestica po kružnici brže giba. To vrijedi ako uspoređujemo gibanje dvaju tijela na različitim polumjerima ali istih obodnih brzina.

Centripetalno ubrzanje razmjerno je polumjeru

Ako, međutim, promatramo gibanje dva tijela na različitim polumjerima ali s istim kutnim brzinama onda će centripetalno ubrzanje biti razmjerno polumjeru, odnosno veće ubrzanje imat će tijelo kojem je veća obodna brzina.

Sile koje koje imaju centripetalni učinak tijelima skreću putanju u kružnicu zato ih nazivamo centripetalne sile. Budući da je sila općenito umnožak mase i ubrzanja tako se i centripetalna sila dobiva množenjem mase i centripetalnog ubrzanja:

F_cp  = 

m v² / r

 =  m ω² r  =  m

4π² / T ²

r  =  m 4π²f ² r

I ovdje ćemo utvrditi da je za kružnu putanju potrebno djelovanje sile, ali bi bilo pogrešno reći da je "centripetalna sila uzrok kružnog gibanja“. Naime centripetalna sila nije uzrok nikakvog gibanja pa niti kružnog zato što centripetalna sila ne može niti jedno tijelo pomaknuti s mjesta niti mu može mijenjati iznos brzine.

Centripetalna sila može samo putanju učiniti kružnom, odnosno ona može mijenjati smjer brzine. No ona nije "pogon" za napredovanje tijela po toj kružnici. Na primjer: Ako bi nogom udarili loptu koja je vezana za kolčić zaboden u zemlju, lopta bi krenula u gibanje po pravcu sve dok joj napetosti niti koja ima centripetalni učinak ne bi putanju savila u kružnicu. Ali pri tome ta centripetalna sila nije uzrok gibanja lopte, jer lopta se giba zato što je udarena nogom, a napetost niti joj samo mijenja smjer brzine. Ako bismo loptu koja miruje na travnjaku počeli povlačiti prema kolčiću, dakle u smjeru centripetalne sile, to ne bi uzrokovalo kruženje lopte. Za ostvarivanje kružne putanje potrebno je da tijelo već ima neku brzinu kojoj će centripetalna sila promijeniti smjer.

 

 

Osim napetosti niti centripetalni učinak može stvarati i pritisak stjenke. Tako na primjer možemo zamisliti da kuglu zakotrljamo u kružnu ogradu. Pritisak ograde skrenut će putanju a time i vektor brzine. Ako bi ograda bila obložena mekanim plastelinom kugla bi utisnula trag kao posljedicu pritiska. No jasno je da pritisak ograde nije uzrok gibanja kugle, ona se giba zato što smo je gurnuli, a centripetalna sila samo skreće smjer vektora brzine.

 

 

 

Centripetalni učinak mogu stvarati i druge sile pa se tako možemo pitati koja sila omogućava automobilu da skreće u zavoju ceste. Odnosno koji uvjeti na cesti uzrokuju da automobil ne može skrenuti nego nastavlja gibanje po pravcu i dolazi do slijetanja s ceste? Očito je iz iskustva da na poledici vozila ne mogu zadržati smjer kružnoga gibanja, iz čega zaključujemo da centripetalni učinak ima sila trenja.

 

 

 

 

 

U magnetskom polju javlja se također jedna sila s centripetalnim učinkom, a djeluje na električne naboje u gibanju. Ako se naboj Q giba brzinom v→ tako da vektor brzine i vektor magnetske indukcije B→ čine neki paralelogram (tj. da nisu paralelni) javlja se sila koja je okomita i na v→ i na B→. Ta se sila zove Lorentzova, a djeluje tako da skreće putanju naboja. Lorentzova sila je razmjerna naboju Q i površini paralelo-grama koji razapinju v→ i B→.

 

 

 

 

Promatrač u ubrzanom sustavu koji se okreće doživljava i vidi inercijalnu silu koja djeluje radijalno od središta vrtnje prema obodu. Ta sila postoji samo za promatrača u tom sustavu i to je centrifugalna sila. Centrifugalna i centripetalna sila jesu isitih iznosa, a suprotnih smjerova i djeluju na isto tijelo ali u različitim sustavima pa stoga ne podliježu 3. Newtonovom zakonu i međusobno se ne poništavaju. O centrifugalnom ubrzanju i centrifugalnoj sili kao i drugim inercijanim silama vidi članak Inercijalno ubrzanje.